Última atualização: segunda-feira, 11 de abril de 2022 17:06

Por que é impossível ganhar na roleta?

Por que você não pode ganhar na roleta online? Neste artigo, apresentamos uma prova matemática da expectativa matemática negativa no curso quando você joga na roleta. Também exploraremos as evidências matemáticas de ineficácia ao usar as estratégias vencedoras. Então, por que é impossível ganhar na roleta? A linha básica é que existem 37 números no campo (0-36) e os pagamentos são pagos 36 a 1. Então, toda vez que você aposta, estatisticamente, você está perdendo 2,7% do valor da aposta (mesmo que tenha ganho no giro atual). Se você quiser verificar nossas explicações matemáticas, leia mais.

• Não importa se você prefere roleta, blackjack ou caça-níqueis, o cassino Fastpay é a melhor escolha para você (mais de 5.000 jogos)

Por que você não consegue ter sucesso na roleta usando estratégias?

Vamos considerar todas as apostas comuns possíveis na roleta como a prova matemática da impossibilidade de ganhar na roleta e determinar seu resultado ME (expectativa matemática).

No caso geral, I de qualquer aposta na roleta pode ser calculado usando a fórmula clássica (1): 

, (1)

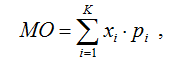
• Onde é xi– evento I,
• Pi– A probabilidade do evento I,
• Ê – O número total de eventos formando um grupo completo.

A expectativa matemática da versão europeia:

A fórmula (1) para ME de qualquer aposta na “roleta européia” pode ser convertida levando em probabilidade total, eventos não colaborativos, ou seja Pwin.+ Ploss.=1, para a visão com o jogo para N setores (quartos), é igual a:
… (2)

Uma vez que a probabilidade de ganhar Pwin na “roleta europeia”, enquanto você joga por N setores (quartos), é igual a:

, que por fim, obtemos a expressão para ME para QUALQUER aposta na “roleta europeia”, quando você está jogando por N setores (quartos), é igual a:

… (3)
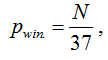
Vamos calcular ME para cada aposta “simples” (básica) na “roleta europeia” (uma roda com um zero). O resultado do cálculo de ME para apostas básicas médias é apresentado na tabela 1.

A expectativa matemática para as apostas:

Tabela 1. Cálculo do ME para apostas “simples”.

№	Aposta «simples»	Vitória		Perda	Cálculo МО, у.е.
		Pagamento	Probabilidade	Probabilidade
1.	Direto	35:1	1/37	36/37	=35×1/37-36/37= -1/37
2.	Dividir	17:1	2/37	35/37	=17×2/37-35/37= -1/37
3.	Rua	11:1	3/37	34/37	=11×3/37-34/37= -1/37
4.	Canto	8:1	37/04	33/37	=8×4/37-33/37= -1/37
5.	Seis Linhas	5:1	37/06	31/37	=5×6/37-31/37= -1/37
6.	Coluna e Dezenas	2:1	37/12	25/37	=2×12/37-25/37= -1/37
7.	Even Chance	1:1	18/37	19/37	=1×18/37-19/37= -1/37

Como podemos ver na tabela – ME é exatamente igual ao valor obtido pela fórmula (3). Vamos resumir os resultados.

O jogador sempre perde mesmo quando ganha

Se o jogador estiver jogando na “roleta européia”, (não importa onde e quanto ele coloca), SEMPRE perde 1/37 parte da aposta (apostas). No mesmo ME do jogo, não depende do resultado do giro; ou seja, o jogador perde mesmo quando ganha. Ou seja, o jogador SEMPRE perde quando faz uma aposta na “Roleta Europeia”, independentemente do resultado da rodada atual.

Usando as estratégias das apostas:

Pela prova matemática da impossibilidade de ganhar em ” roleta europeia ” ou ” Roleta Americana ,” é o suficiente para expandir qualquer estratégia de apostas na aposta “básica”. Como o resultado ME de todas as apostas é negativo e igual a -1/37 do tamanho da aposta, então a expectativa total do resultado do jogo será negativa e igual a -1/37. A soma de todas as apostas feitas pelo jogador ou -1/37 do valor da aposta média multiplicado pelo número de rodadas jogadas por um apostador.

Avaliar o ME de qualquer estratégia é suficiente para determinar o valor da aposta média enquanto você está jogando de acordo com esta estratégia e levando em consideração todas as regras de transição de aposta para aposta, e multiplicando o resultado por -1/37. O valor da aposta média e a soma de todas as apostas são valores positivos; portanto ME é sempre menor que zero, ou seja ME£0 e menor que ME£-1/37 se usada a progressão porque a taxa média é maior que 1.

Dispersão

Vamos calcular a variância para qualquer aposta na “roleta européia”, dependendo de quantos setores N (quartos) coloca o jogador. Use a variância determinar o critério ideal do Bank Kelly para jogar “roleta europeia”.

Informações

Banco no critério de Kelly mostra qual deve ser o banco do apostador para o saldo total de todos os jogos aspirados ao infinito.

No caso geral, a variância do jogador que está jogando na “roleta européia” em N setores (salas) pode ser calculada pela expressão:

. (4)

A fórmula (4) para a variância D de quaisquer apostas na “roleta europeia” pode ser convertida considerando a probabilidade total, não eventos conjuntos, ou seja, Pwin.+ Ploss.=1, para a mente:

. (5)

Já que a probabilidade de ganhar Pwin na “Roleta Europeia” enquanto você joga por N setores (quartos) é igual a:

, finalmente, obtemos a expressão para a dispersão D de qualquer aposta na “roleta europeia” quando você está jogando em N setores (quartos), é:

. (6)

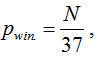
A magnitude da dispersão D tem um valor positivo em toda a gama de jogos em N setores. Isso é um detalhe importante.

Onde é possível calcular o banco necessário para o jogo na “roleta europeia” usando o critério de Kelly:

. (7)

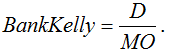
Usando as expressões (3) e (6), finalmente obtemos a expressão:

(8).

A fórmula (8) mostra que o valor ótimo do banco, segundo Kelly critério para jogar na “Roleta Europeia” é um valor negativo.

Conclusão:

Se o valor ótimo do banco do jogador seguindo o critério de Kelly for negativo, então jogar na “roleta europeia” geralmente não é necessário, uma vez que o resultado geral do saldo de todos os jogos dos jogadores se aproxima de zero, ou o jogador perderá todo o seu dinheiro durante o longo jogo.

Para avaliar a “atratividade” do jogo, pode-se usar critérios generalizados, que são obtidos como a relação entre o banco exigido do jogador seguindo o critério de Kelly e a expectativa matemática do resultado do jogo, ou seja:

(9).

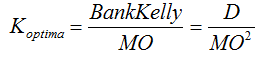
Com esta expressão (9) pode-se entender que quanto menor o tamanho do banco do apostador na expectativa matemática, “melhor” será o jogo para o jogador. Este critério ótimo pode ser interpretado como o critério do mínimo banco específico do jogador por unidade de lucro do jogo.

Os critérios ótimos do jogo Кoptima só podem ser usados ​​para avaliação de jogos com expectativa positiva! Se o jogo tiver um MT negativo, não atrairá a atenção dos apostadores. Para a “roleta europeia” MT -1/37, isso é menor que zero, portanto, a “roleta europeia” como jogo não é “atraente” para os jogadores. É por isso que é impossível ganhar na roleta, independentemente das estratégias de apostas e seleção de táticas de itens que você usa.

Nota: as fórmulas (3), (5) e (8) podem ser obtidas para a “roleta americana” com dois setores de zero: 0 e 00.

Materiais semelhantes

• Jogue roleta europeia grátis da NetEnt
• Por que a casa do cassino sempre ganha?
• Como ganhar na roleta.

Onde jogar?

• Escolher um honesto é um passo importante antes de começar a jogar em jogos ao vivo ou slots. Nosso altamente recomendado é o cassino Fastpay . Eles enviarão o dinheiro em 5 minutos.

Confira os melhores cassinos online 2022

Adicionar comentário

Enviar

Cancelar